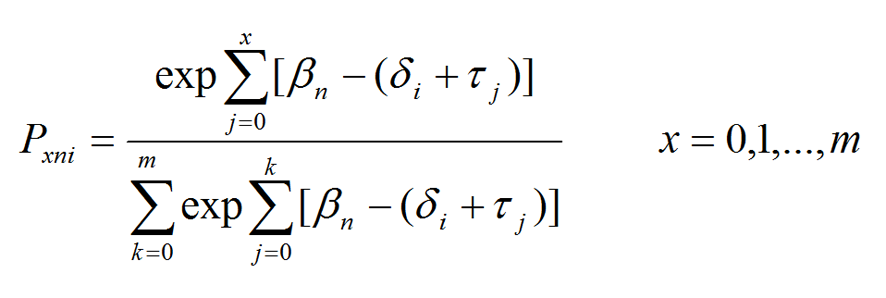Foreign language anxiety (FLA) has been defined by Horwitz, Horwitz, and Cope (1986) as “a distinct complex of self-perceptions, beliefs, feelings and behaviors related to classroom language learning which arise from the uniqueness of the language learning process” (p. 128). Horwitz et al. (1986) suggest that it can be helpful to draw parallels between FLA and three performance related anxieties: (1) communication apprehension, (2) test anxiety, and (3) fear of negative evaluation. MacIntyre and Gardner (1989) tested Horwitz et al.’s model of language anxiety and stated that these three dimensions do indeed contribute to language anxiety.
It is important to investigate, understand and address FL classroom anxiety as anxiety contributes to an affective filter hindering the learner’s ability to absorb the target language and thus language acquisition fails to advance (Krashen as cited in Horwitz et al., 1986). To date, FLA studies have not been conducted in Cyprus but it is well documented that language anxious students often exhibit avoidance behaviours such as missing class and postponing homework (Horwitz et al., 1986). Some report problems such as the pace of the class being too fast and that they feel left behind (MacIntyre & Gardner, 1991).
At the output stage, anxiety may obstruct retrieval of previously learned information (Tobias, 1986). Indeed, although language-anxious students study more than their low-anxious counterparts, their level of achievement often does not reflect that effort (Horwitz et al., 1986; Price, 1991; Tsai & Li, 2012). This negative correlation between anxiety and performance has been reported by many researchers (e.g., Horwitz, 1986; MacIntyre & Gardner, 1991). Conversely, Kleinmann (1977) reported a positive relationship between anxiety and performance.
The Foreign Language Classroom Anxiety Scale (FLCAS; Horwitz et al., 1986) has been used in studies extensively over the past 27 years and has facilitated a tremendous development in the research into FL classroom anxiety. Notwithstanding, instruments should always be piloted for new settings and new populations as “existing validity evidence becomes enhanced (or contravened) by new findings” (Messick, 1993, p. 13). This study is the first, to the authors’ knowledge, to validate the FLCAS (Horwitz et al., 1986) for Cypriot senior high school students of English.
Literature Review
The Foreign Language Classroom Anxiety Scale
In 1986 Horwitz et al. developed the Foreign Language Classroom Anxiety Scale (FLCAS) to measure anxiety specific to a foreign language classroom setting. According to Horwitz (1986), in designing the instrument Horwitz et al. (1986) drew on measures of test anxiety (Sarason, 1978), speech anxiety (Paul, 1966), and communication apprehension (McCroskey, 1970) as well as including five items from the French Class Anxiety Scale (Gardner, Clement, Smythe, & Smythe, 1979). The FLCAS consists of 33 items and uses a five-point Likert scale (“strongly disagree” to “strongly agree” with a neutral category in the middle). Possible scores on the FLCAS range from 33 to 165. The higher the score, the higher the level of foreign language anxiety experienced.
Sarason defines test anxiety as “the tendency to view with alarm the consequences of inadequate performance in an evaluative situation” (as cited in Aida, 1994, p. 157). Aida (1994) and Julkunen (as cited in Aydin, 2009) found that test anxiety is a significant variable in the language learning process.
Factor Structure of the FLCAS
In the original study, Horwitz et al. (1986) reported a Cronbach’s alpha of 0.93 (N = 108) and a test-retest correlation of .83 (N = 78). Criterion related studies showed that FLCAS scores had the highest correlation with test anxiety, 0.58. Since then the majority of studies have relied on alpha (e.g., Truitt, 1995 as cited in Kim, 2009; Wei, 2007) and principal components analyses to investigate the validity of the FLCAS.
Studies so far have shown different factor structures for the FLCAS. It is of fundamental importance to establish whether the factors or dimensions comprising the scale are correlated between them for if they are not then the scale cannot be used to measure a single construct, namely “foreign language classroom anxiety”. Horwitz et al. (1986) implied a three factor structure. Tóth (2008) used the FLCAS on a Hungarian sample and verified the three components suggested in Horwitz et al. (1986) and confirmed that test anxiety is one of the components. Tóth (2008) also claimed that the factors obtained were closely related thus confirming that FLCA is a unidimensional construct. On the other hand, Aida (1994) found four factors for the FLCAS in a sample of 96 American students learning Japanese. A few years later Cheng, Horwitz, and Schallert (1999) extracted two factors as did Matsuda and Gobel (2004). They labelled the first factor General English Performance Anxiety and the second Low Self-Confidence in Speaking English.
It is noteworthy that the original three constructs that Horwitz et al. (1986) posited in developing the measure did not emerge as factors of the FLCAS in three subsequent studies (Aida, 1994; Cheng et al., 1999; Matsuda & Gobel, 2004). In fact the latter researchers questioned whether test anxiety items should be included in the scale as, according to their findings, it did not emerge as a factor.
Apple (2011) states, “Unfortunately the items of the FLCAS were never validated and the unidimensionality of the FLCAS was never examined, even though the originators admitted to deliberately including items from what they believed were three separate constructs” (p. 58). This is an important issue which must be addressed. He extracted the 11 items related to communication apprehension and validated these using Rasch methods. Bora and Jongmin (2011) used Item Response Theory (IRT) to show that the FLCAS is unidimensional and reliable. They further reported that the FLCAS provides precise and reliable information for persons with low to medium levels of language anxiety whereas information becomes increasingly unreliable for individuals having high levels of anxiety.
If the scale is found to be multidimensional this makes using one total score questionable and it would be advisable for future researchers to try three separate scores for the three components (or two or four depending on the number of factors extracted) and investigate them separately.
Reliability and Length of a Scale
Most studies on the FLCAS place, as mentioned earlier, heavy emphasis on Cronbach’s alpha, the most popular measure of internal consistency. However, since alpha is influenced by the number of items and parallel repetitions of items, many scale designers fall into the trap of including too many items in an attempt to achieve high alphas. Boyle (1985) argues that high values of alpha may be an indication of item redundancy and narrowness of the scale. Lengthy scales can be cumbersome for respondents and “can result in an extended time to survey completion, a greater amount of missing data and lower response rates…. They may also increase random or systematic error associated with fatigue or boredom” (Maloney, Grawitch, & Barber, 2011, p. 162). More importantly however, some lengthy scales may include items that relate weakly to the construct (increasing alpha at the same time), or items with high item total and inter-item correlations which cover a narrow range of the construct under investigation, causing construct underrepresentation and thus lowering the degree of validity of the scale.
Scale constructors should therefore consider looking for ways to reduce the number of items in an attempt to reduce the strength of the obstacles that threaten the validity of the scale. Boyle (1991) suggests that items selected should have a high loading on the factor measured by the scale but at the same time should exhibit moderate to low item inter-correlations in order to maximise the breadth of measurement of the construct. Merely including additional items in a scale ignores the error variance associated with each item and should be regarded as being an unsophisticated method of increasing scale reliability. Boyle (1991) concludes his article by stating: “However, especially in the non-ability areas of motivation, personality and mood states, moderate to low item homogeneity is actually preferred if one is to ensure a broad coverage of the particular construct being measured” (p. 292).
On a similar note Kline (1979, p. 3) states that “each part of the test must be measuring something different … A higher correlation than 0.7 on the other hand suggests that the test is too narrow and too specific … if one constructs items that are virtually paraphrases of each other, the results would be high internal consistency and very low validity”.
One approach to identifying items weakly related to the construct measured (with the use of the fit statistics) or parallel items (with the item statistics and item placement on the construct continuum) and to help reduce the scale length without loosing its psychometric properties is Rasch measurement.
Rasch Measurement
The Rasch Models
The Rasch model asserts that a person with higher ability (in the case of this study, endorsability, i.e., higher position on the FLCA continuum) always has a higher probability of endorsing any item than a person with lower ability, and a more difficult (to endorse) item has a lower probability of endorsement than a less difficult item, regardless of person position on the FLCA continuum. The original breakthrough by Rasch in 1960 has been developed and extended to address every reasonable observational situation in the social sciences (Andrich, 1978; Masters, 1982). If the test has a single type of item, with the same number of marks available (as with the Likert scales), then the Rating Scale Model (RSM) applies (Andrich, 1978).
According to the model the probability of a person n responding in category x to item i, is given by:
where το = 0 so that βn is the person’s position on the variable, δi is the scale value (difficulty to endorse) estimated for each item i and τ1, τ2, . . ., τm are the m response thresholds estimated for the m + 1 rating categories.Panayides, Robinson, and Tymms (2010) reported quite a few examples of applications of the Rasch models, showing the diversity of social sciences situations in which they can be used productively, including construction and evaluation of psychometric scales.
Unidimensionality
An important issue in the validation of any psychometric scale is the investigation of its dimensionality. Scales where single scores are used to position individuals on a latent trait continuum should be unidimensional. Factor analysis (FA) is the statistical technique which is widely used in psychometrics to investigate the dimensionality of empirical data.
The Rasch model on the other hand, constructs a one-dimensional measurement system from ordinal data regardless of the dimensionality of the data. If the response patterns indicate the presence of two or more dimensions so disparate or distinct that it is no longer clear what latent dimension the Rasch model defines, then unidimensionality is breached. FA “is confused by ordinal variables and highly correlated factors. Rasch analysis excels at constructing linearity out of ordinality and at aiding the identification of the core construct inside a fog of collinearity” (Schumacker & Linacre, 1996, p. 470). Linacre (1998) showed that Rasch analysis followed by Principal Components Analysis (PCA) of standardized residuals is always more effective at identifying multidimensionality than direct FA of the original response-level data.
An important issue for the presence of a second dimension is the choice of the critical value of its eigenvalue. Researchers have suggested various critical values such as 1.4 (Raîche, 2005; Smith & Miao, 1994) or 1.5 (Smith, 2004). Linacre (2005) however, argues convincingly that an eigenvalue less than 2 indicates that the implied dimension in the data has less than the strength of two items, and so, however powerful it may be diagnostically, it has little strength in the data. Linacre explains with an example that perhaps more importance must be placed on the strength of the factors and not on the magnitude of their eigenvalues. In concluding he gives some general rules of thumb; one concerning the eigenvalues is that in the unexplained variance a secondary dimension must have the strength of at least 3 items. If a factor has eigenvalue less than 3 (in a reasonable length test) then the test is probably unidimensional.
Therefore, in Rasch analyses, where PCA is carried out on the standardised residuals and not the original observations the first dimension has already been removed. One looks at the first dimension (or contrast) extracted. Linacre (2005) suggests looking at the content of the items at the top (with the highest positive loadings on the contrast) and bottom (with the highest negative loadings on the contrast). The number of items to look at depends on the eigenvalue. For example if the eigenvalue is 3 then look at the top three items and the bottom three items. If these items are different enough, in content, to be considered different dimensions then split the data into separate analyses. If the items are part of the same dimension then no action is necessary.
Fit Statistics
Two mean square statistics are used in Rasch analyses, the infit and the outfit. The fit statistics report how well the data fit the unidimensional framework that the Rasch analysis has constructed. Therefore, they report the degree to which the observations meet this vital specification of measurement. Linacre and Wright (1994) explain that the outfit statistic is dominated by unexpected outlying, off-target, low information responses. The infit statistic is an information-weighted sum, introduced to reduce the influence of outliers. It is dominated by unexpected inlying patterns among informative, on-target observations.
This Study
Setting
The Cypriot educational system is highly centralised. Teacher appointments, postings, promotions, curriculum and teaching materials are all dictated by the Cypriot Ministry of Education and Culture.
Schooling is separated into primary (six years), lower secondary (three years) and upper secondary (three years). Upper secondary is optional and those students opting to stay on, have a choice between academic, technical and catering school.
English-as-a-Foreign-Language Education in Cyprus
English is the most commonly studied foreign language in many countries, including Cyprus. Ioannou-Georgiou and Pavlou (1999) map the history of the English language in Cyprus. Cyprus was a British colony from 1878 to 1960. English was introduced to the curriculum in the final two classes of the larger schools in 1935. Following independence in 1960, emphasis was placed on the learning of a foreign language and due to the island’s close relations with Britain, English was chosen. In 1965-66 the teaching of English became compulsory and pupils began learning English from the age of nine-ten with two periods a week and continued until they completed secondary education (at 18 years of age). In 1992 the ministry of Education introduced the teaching of English in the fourth year of primary school (age eight to nine) with one 40-minute period a week. Since 2002, English is now optional in the final two years of school. Students are required to study any two of a choice of seven languages for a minimum of two periods each. Five of these languages are “new” to them. Students who select English in the final two years choose a course of either two periods a week (the core course) or six periods a week (the advanced course). In September 2011, English was introduced into the curriculum for first year primary school pupils (age five to six).
Research Questions
The purpose of this study was to assess the psychometric properties of the FLCAS for Cypriot senior high school students of EFL with the use of Rasch measurement. Validations have hitherto concentrated on university students. Since “teenagers are the most insecure people in the world, their lives vulnerable to a host of different pressures” (Scheidecker & Freeman, 1999 as cited in Dörnyei, 2001, p. 87) it is pertinent that more attention be given to assessing and addressing FLCA in this age group.
In this study the following research questions were investigated:
-
Is the FLCAS a unidimensional scale?
-
Does the FLCAS provide reliable measures? (The term “measures” is used rather than scores in order to emphasise the ability of the Rasch models to provide linear measures as opposed to raw scores obtained from counting observed scores.)
-
Is the 5-point Likert scale psychometrically optimal?
Apparent inconsistencies in research findings such as those of MacIntyre and Gardner (1989) and Aida (1994) which found test anxiety not to be conceptually related to other components of FLA, as Horwitz et al.’s (1986) theory had proposed, and suggestions that items reflective of test anxiety could be eliminated from the FLCAS call for further research. Rasch methods will clear up this discrepancy through the investigation of the dimensionality of the scale in the context of the first research question.
Methodology
Participants
The present study involved a total of 304 randomly selected EFL students (ages 16-18) from three senior high schools in Limassol, Cyprus. The students have all been studying English for a minimum of eight years. Following comprehensive explanations of the purpose of the study, permission to administer questionnaires was attained from the relevant head-teachers.
The Instrument
Permission was also attained from Dr. Elaine Horwitz for the use of the FLCAS for the purpose of this study. The FLCAS was translated into Greek by an official translator and edited by the researchers so as to carry the meaning of the original instrument. Subsequently the Greek version was given to two experienced EFL teachers, who are native speakers of Greek, to translate back into English to confirm that the meaning had not been altered. The scale contained 9 negatively worded items, the scores of which were reversed prior to analyses.
The Rasch Measurement Approach
Selection of the Rasch Rating Scale Model (RSM)
The Rasch RSM was selected for the analysis of the FLCAS data because of the following advantages over other IRT models. First, the Rasch models are the only models that accept the raw scores of the respondents to be a sufficient statistic for the estimation of their position on the variable continuum thus maintaining the score order of students. Since raw scores are the basis for reporting results in all previous studies on FLCA, the Rasch models are consistent with practice. Second, the Rasch models involve fewer parameters and are thus easier to work with, to understand and to interpret. Third, the Rasch models give stable item estimates with smaller samples than other more general IRT models (Thissen & Wainer, 1982). Fourth, the person measures and item calibrations have a unique ordering on a common logit scale (Bond & Fox, 2001, 2007; Wright & Masters, 1982) making it effortless to see relations between them. Fifth, validity and reliability issues can be addressed through the use of the Rasch models (Smith, 2004).
Most importantly, the philosophy of the Rasch model dictates the structure of the data including the fact that unidimensionality is necessary for the measurement process. Other models try to model all the characteristics observed in the data, regardless of whether they contribute to the measurement process. So, “the difference is between measurement and modelling. If the aim is to construct a good measure then the items comprising the scale should be constrained to the principles of measurement, thus the Rasch model is highly appropriate” (Panayides & Walker, 2012, p. 333).
Estimation Method
WINSTEPS (Linacre, 2005) was used for the analysis of the data. WINSTEPS uses Joint Maximum Likelihood Estimation in preference to Conditional Maximum Likelihood Estimation or Marginal Maximum Likelihood Estimation “because of its flexibility with missing data. It also does not assume a person distribution” (Linacre, 2005, p.11). Any estimation bias is not a real concern as, except in rare cases where exact probabilistic inferences are to be made from short tests or small samples.
Selection of the Fit Statistics
The infit mean and outfit mean square statistics were preferred for this study, over a large number of fit statistics, for their exploratory nature (Douglas, 1990). They can identify a wide range of potential sources of unexpected response patterns and this is an advantage in the sense that a fit statistic that focuses on a specific type of unexpectedness may not have enough power to identify other types, thus missing “bad” items. Also, they have been used successfully to assess the fit of the Rasch models for many years (e.g., Curtis, 2004; Lamprianou, 2006; Panayides & Walker, 2012; Smith, 1990; Wright & Masters, 1982). Furthermore, these statistics are computationally simpler and stand up well in comparison with possibly more precise tests, therefore there is no practical reason to use anything more complicated (Smith, 1990). Finally, they are utilized by most Rasch software packages (e.g., Quest, Winsteps, Facets) and are familiar to many researchers.
Critical Values for the Fit Statistics
Wright, Linacre, Gustafson, and Martin-Lof (1994) and Bond and Fox (2001, 2007) provide a table of reasonable item mean square fit values and suggest a critical value of 1.4 for scales, indicating 40% more variability than predicted by the Rasch model. Curtis (2004) and Glas and Meijer (2003) suggest using simulated data according to an IRT model based on the estimated parameters and then determining the critical values empirically. However, Lamprianou (2006) argues that misfit is not a dichotomous “yes”/“no” property but rather a matter of degree and as such it can be considered too large for one study and satisfactory for another depending on the aims of the researchers. For the purposes of this study, the widely used cut-off value of 1.4 was used as suggested by Wright et al. (1994) and Bond and Fox (2001, 2007).
Reliability Indices
The person reliability indicates the precision of the scale by showing how well the instrument distinguishes individuals. It can be replaced by the person separation index which ranges from zero to infinity and indicates the spread of person measures in standard error units (Wright & Masters, 1982).
Rasch Diagnostics for the Optimal Number of Categories
A critical component influencing the measurement properties of any self-reported psychometric scale is the rating scale. Yet there is no general agreement regarding the optimal rating scale format. Khadka, Gothwal, McAlinden, Lamoureux, and Pesudovs (2012), in a study investigating 17 instruments, reported that scales with complicated question format, a large number of response categories or unlabelled categories tended to be dysfunctional. They developed guidelines on the design of rating scales, suggesting a maximum of five, clearly-labelled and non-overlapping categories. Wright and Linacre (1992) state that it is the analyst’s task to extract the maximum amount of useful meaning from the responses observed by combining (or even splitting) categories if necessary based on the results of careful analysis. Furthermore, they advise researchers that in combining two or more categories they must be sure it is reasonable to do so, and that both the statistical and substantive validity of the results are improved. Rasch analysis provides a strong tool in the assessment of the functioning of rating scales.
Linacre (2002) suggested the following guidelines for determining the optimal number of categories for a given scale. First, categories with low frequencies (lower than 10) are described as problematic because they do not provide enough observations for estimating stable threshold values. Second, the average measures (the average of the ability estimates of all persons in the sample who chose a particular category) are expected to increase monotonically in size as the variable increases. This indicates that on average, those with higher scores on the FLCA variable endorse the higher categories. Third, the thresholds, or step calibrations (the difficulties estimated for choosing one response category over another) should also increase monotonically across the rating scale. If they do not, they are considered disordered. Fourth, the magnitudes of the distances between adjacent threshold estimates should indicate that each step defines a distinct range on the variable.
Linacre (2002) suggests that thresholds should increase by at least 1.4 logits (in the case of a 3-point scale), to show distinction between categories, but not more than 5 logits, so as to avoid large gaps in the variable. For a 5-point rating scale Linacre suggests at least 1.0 logits distance between adjacent thresholds for a distinct range on the variable continuum. Step disordering and very narrow distances between thresholds “can indicate that a category represents too narrow a segment of the latent variable or corresponds to a concept that is poorly defined in the minds of the respondents” (Linacre, 2002, p. 98). Finally, the fit statistics provide another criterion for assessing the quality of a rating scale. Outfit greater than 2 indicates more misinformation than information, thus the category introduces noise into the measurement process.
Results
Preliminary Analyses
Raw score comparisons with other studies
Table 1 shows the descriptive statistics of this study together with four primary studies on the FLCAS.
Table 1
Comparisons of This Study With Results From Four Primary Studies
| Aida (1994) | Horwitz et al. (1986) | Cao (2011) | Bekleyen (2004) | This study | |
|---|---|---|---|---|---|
| Sample size | 96 | 108 | 300 | 115 | 304 |
| Language | Japanese | Spanish | English | Five different | English |
| Sample age | University students | University students | University students | University students | 16–18 years |
| Alpha | 0.94 | 0.93 | 0.95 | 0.90 | 0.96 |
| Range of scores | 47 – 146 | 45 – 147 | Not reported | 55 – 145 | 34 – 153 |
| Mean score | 96.7 | 95.5 | Not reported | Not reported | 76.9 |
| St. deviation | 22.1 | 21.4 | Not reported | Not reported | 25.9 |
Extremely high alphas (greater than or equal to 0.90) were found in all four studies presented in Table 1 as well as in this study. Only one study reported alpha below 0.90, Matsuda and Gobel (2004), who reported 0.78. The range of total scores was slightly larger in this study and so was the standard deviation. However, the mean score was significantly lower. There are two possible explanations for this difference. First, English is so widely used in Cyprus (TV, computers, mobile telephones, advertisements, tourism) that students of this age have plenty of exposure to the language. Second, the sample consisted of students who have been learning English for between eight and ten years.
The Preliminary Reliability Investigation
Before commencing the Rasch analyses a reliability analysis was carried out with the use of Cronbach’s alpha to gain a first impression of the items. Nunnally (1978) recommends that instruments used in basic research have reliability of about 0.70 or better. He adds that there is no reason for increasing reliabilities much beyond 0.80. On the other hand, where important decisions about the fate of individuals are made on the basis of test scores, reliability should be at least 0.90, preferably 0.95.
Alpha in this study was found to be 0.958 and that is an extremely high value of internal consistency for psychometric scales. It should also be noted that the corrected item-total correlation of items 2, 5, 6, 17 and 22 were 0.439, 0.236, 0.151, 0.321 and 0.407. These were the lowest correlations; all others were above 0.5 with 15 of them having correlations higher than 0.70. Kline (1979) argued that correlations higher than 0.7 are not too desirable because this suggests that the scale is too narrow in construct coverage. “If one constructs items that are virtually paraphrases of each other, the results would be high internal consistency and very low validity” (Kline 1979, p. 3). The Rasch approach has the ability to clarify this point.
Rasch Analyses
First and Second Calibrations
The first calibration of the full dataset (33 items and 304 students) revealed five misfitting items, the same items noted above in the preliminary reliability analysis. Four of these items were badly misfitting, with infit and/or outfit mean square statistics above 2.0. Table 2 shows the misfitting items, their measure and standard error, their infit and outfit mean square statistics and their point measure correlation.
Table 2
Misfitting Items in Misfit Order
| Items | Measure | St. error | Infit | Outfit | Pt.meas. correlation |
|---|---|---|---|---|---|
| 5 | 0.31 | 0.07 | 2.07 | 2.39 | 0.28 |
| 17 | -0.31 | 0.06 | 1.73 | 2.20 | 0.37 |
| 6 | -1.27 | 0.06 | 1.99 | 2.19 | 0.23 |
| 22 | -0.41 | 0.06 | 1.58 | 2.15 | 0.44 |
| 2 | -0.20 | 0.06 | 1.37 | 1.60 | 0.48 |
The misfit on the four badly misfitting items was mainly caused by unexpectedly high scores from students with estimated FLCA much lower than the item difficulty. For example student 56 with estimated FLCA of – 2.24 scored four on item 5 with difficulty estimate of 0.31, and student 171 (estimate of – 2.46) scored five on item 17 (difficulty – 0.31).
Further analysis of the content of the items was undertaken. None of the items refer to anxiety per se. Item 5 (It wouldn’t bother me at all to take more foreign language classes) was a reversed item. It refers to language classes in general and not specifically English classes, as is the focus of this study, but more importantly it does not necessarily measure anxiety. The reason for not wanting to take more foreign language classes could be greater interest in other subjects, such as science subjects. Item 17 (I often feel like not going to language classes) could be considered to be relevant to factors other than FLCA, such as lack of motivation, indifference or more interest and inclination for other subjects. Item 6 (During language class, I find myself thinking about things that have nothing to do with the course) is again a general item that is not necessarily related to FLCA. It could be pertinent to lack of motivation or even indicative of Attention Deficit Hyperactivity Disorder. Finally, item 22 (I don’t feel pressure to prepare very well for language class) could be indicative of high ability, lack of challenge, interest or motivation.
These four badly misfitting items were removed since infit or outfit values greater than two indicate that the items are introducing more noise than information into the measurement process. The data was calibrated again and this time item 2 had a much worse misfit (outfit 1.95 and infit 1.57). Item 2 (I don’t worry about making mistakes in language class) is another reversed item which could refer to competence or indifference rather than anxiety. Therefore, item 2 was also removed.
Third and Final Calibrations
The third calibration revealed 13 persons with infit and/or outfit greater than 3.0. The aberrant responses of these students were badly distorting the measurement process and were removed leading to the final calibration with 28 items and 291 students.
Reliability
The person reliability was 0.93 and this was still questionably high. Such high reliabilities are possible when the item estimates are very widely spread with a large variance and targeted well at the distribution of person estimates. The person separation index was also high (3.64).
Dimensionality
Table 3 shows the results of the PCA of the standardised residuals.
Table 3
Standardized Residual Variance (in Eigenvalue Units)
| Empirical | (%) | Modeled (%) | ||
|---|---|---|---|---|
| Total raw variance in observations | 57.8 | 100.0 | 100.0 | |
| Raw variance explained by measures | 29.8 | 51.6 | 52.4 | |
| Raw variance explained by persons | 25.9 | 44.8 | 45.5 | |
| Raw Variance explained by items | 3.9 | 6.8 | 6.9 | |
| Raw unexplained variance (total) | 28.5 | 48.4 | 100.0% | 47.6 |
| Unexplained variance in 1st factor | 2.5 | 4.4 | 9.0% |
To judge the strength of the measurement dimension, the variance explained by the measures was found to be 51.6% of the total variance in the data. The first factor had an eigenvalue of 2.5 and the strength of less than three items.
In an attempt to investigate the possible presence of a second dimension the content of the three items with the highest positive and the three items with the highest negative loadings on the first factor was compared. Table 4 shows those six items with their corresponding loadings.
Table 4
Content of Items With Highest Positive and Negative Loadings on First Contrast
| Item no | Item Description | Loading |
|---|---|---|
| 20 | I can feel my heart pounding when I'm going to be called on in language class | 0.58 |
| 27 | I get nervous and confused when I am speaking in my language class | 0.48 |
| 26 | I feel more tense and nervous in my language class than in my other classes | 0.42 |
| 11 | I don't understand why some people get so upset over foreign language classes | -0.50 |
| 32 | I would probably feel comfortable around native speakers of the foreign language | -0.47 |
| 14 | I would not be nervous speaking the foreign language with native speakers | -0.44 |
The two sets of items are not different enough in content to be considered different dimensions. The reason for this separation is simply the fact that the bottom three are reversely worded, and this is another strength of the Rasch models, their ability to identify differences in the direction of the items even when they measure the same construct.
Furthermore, Table 3 reveals that the variance explained by the first factor was 9.0% of the unexplained variance and only 4.4% of the total variance. Also, the main dimension measured by the scale has approximately 12 times the strength of the first factor.
Item Fit
Three items were found to be misfitting, item 10 (outfit 1.84, infit 1.76), item 32 (outfit 1.60) and item 8 (outfit 1.51). The question arises as to whether these items should be removed and if so, when does one stop removing misfitting items? Linacre (2010) suggests that if the removal of items is to improve the measures of persons to pursue the following strategy: Estimate the person measures from the original analysis. Remove all items (and/or persons) that are badly misfitting. Then estimate the person measures again and cross-plot the measures from the two occasions. If there are no significant differences in the person measures (that is, points are closely scattered to a straight line and the correlation coefficient is high) then the items are acceptable, otherwise remove the items and repeat the procedure.
Following Linacre’s suggestion the person measures were estimated using the 28 items and then the procedure was repeated with 25 items (removing items 10, 32 and 8). The person measures from the two different item sets were then cross-plotted and Figure 1 shows the plot.
The points are indeed very closely scattered around a straight line. The correlation between the two sets of measures is very high at 0.985. Therefore, there is no negative effect of the inclusion of the three misfitting items on the person measures and these person measures can be considered statistically valid.
Is Foreign Language Test Anxiety (FLTA) a Component of FLCA?
Three analyses were conducted to clear up this discrepancy. Prior to the Rasch analyses two scores were calculated: the sum of the responses to the four remaining test anxiety items (item 2, a test anxiety item, was one of the five items removed after the first calibrations) and the sum of the responses to the remaining 24 items of the 28-item FLCAS. The correlation between the two scores was very high at 0.831 (p < 0.001).
Then, following Linacre’s (2010) recommendation again, the person measures were estimated using the 28 items and the procedure was repeated with 24 items (removing the four test anxiety items, namely items 8, 10, 19 and 21 in Table 6). The person measures from the two different item sets were then cross-plotted and Figure 2 shows this plot.

Figure 1
Cross plot of two sets of person measures (25 items against 28 items).

Figure 2
Cross plot of two sets of person measures (24 items against 28 items).
The points are very closely scattered around a straight line and the correlation between the two sets of measures is very high (0.989). Therefore, there is no negative effect of the inclusion of the four test anxiety items on the person measures and these person measures can be considered statistically valid.
The final analysis is an extension of Linacre’s suggestion and very similar to the method suggested by Smith (2002). Since the interest is on the impact of the four test anxiety items on the validity of persons’ measures, the t-values for the difference between the two measures were calculated (t-values are simply the test statistics used for the very familiar t-test). The formula is
Where bi(28) and bi(24) are the estimates of the measures of person i from the 28-item FLCAS and the 24-item FLCAS respectively and s.e.i(28) and s.e.i(24) their corresponding standard errors. A 95% confidence interval for these t-values would be approximately from -2 to 2. Therefore any values outside this range can be considered as indicating significant differences between the two person measure estimates.
Table 5 shows details of the distribution of these t-values. The range lies between -1.25 and 1.35 with a mean value of 0.198 and standard deviation of 0.344.
Table 5
Descriptive Statistics of the Distribution of the t-Values
| N | Min | Max | Mean | Std. Dev. | |
|---|---|---|---|---|---|
| t-statistic | 291 | -1.25 | 1.35 | 0.198 | 0.344 |
None of the t-values are outside the range from -2 to 2, indicating that all person estimates are statistically equivalent confirming the statistical validity of the measures. These three analyses, together with the good fit of the items to the Rasch model and the results of the PCA of the standardised residuals provide strong evidence that test anxiety is not a second dimension but rather a component of FLCA.
Item Targeting and Spread
Figure 3 shows the person-item map.

Figure 3
Item-person map.
The figure reveals two important facts. The items, with a mean difficulty of 0, are targeted at the higher-scoring students, with measures above the average person measure (-1.06). Furthermore there is a narrow spread of the item positions on the variable continuum, from just above the person mean measure to about one and a half standard deviations above it.
Figure 4 shows the implication of the bad targeting of the items and their narrow spread on precision. The figure depicts the relationship of the error of persons’ estimates (on the vertical axis) against the persons’ measure (on the horizontal axis).

Figure 4
Error of measurement against person measure.
It is clear that the smallest error (and thus the most precise person estimates) lie between around -1.0 logits and +1.0 logits. Large errors are reported for persons with measures below -2.0 logits and above +2.0 logits.
Further investigation was deemed necessary on this narrow spread of the items. Table 6 shows the items in measure (difficulty) order, from highest to lowest together with the point measure correlations.
Table 6
Items in Measure Order
| Items | Description | Measure | Ptmeas |
|---|---|---|---|
| 3 | I tremble when I know that I'm going to be called on in language class | 0.68 | 0.60 |
| 26 | I feel more tense and nervous in my language class than in my other classes | 0.58 | 0.68 |
| 21 | The more I study for a language test, the more confused I get | 0.55 | 0.64 |
| 12 | In language class, I can get so nervous I forget things I know | 0.52 | 0.67 |
| 31 | I am afraid that the other students will laugh at me when I speak the foreign language | 0.39 | 0.67 |
| 16 | Even if I am well prepared for language class, I feel anxious about it | 0.35 | 0.66 |
| 4 | It frightens me when I don't understand what the teacher is saying in the foreign language | 0.26 | 0.63 |
| 20 | I can feel my heart pounding when I'm going to be called on in language class | 0.26 | 0.70 |
| 25 | Language class moves so quickly I worry about getting left behind | 0.26 | 0.68 |
| 27 | I get nervous and confused when I am speaking in my language class | 0.18 | 0.75 |
| 13 | It embarrasses me to volunteer answers in my language class | 0.17 | 0.69 |
| 9 | I start to panic when I have to speak without preparation in language class | 0.04 | 0.70 |
| 24 | I feel very self-conscious about speaking the foreign language in front of other students | 0.03 | 0.68 |
| 19 | I am afraid that my language teacher is ready to correct every mistake I make | -0.05 | 0.68 |
| 1 | I never feel quite sure of myself when I am speaking in my foreign language class | -0.06 | 0.63 |
| 29 | I get nervous when I don't understand every word the language teacher says | -0.06 | 0.72 |
| 7 | I keep thinking that the other students are better at languages than I am | -0.08 | 0.69 |
| 18 | I feel confident when I speak in foreign language class | -0.15 | 0.76 |
| 28 | When I'm on my way to language class, I feel very sure and relaxed | -0.15 | 0.63 |
| 33 | I get nervous when the language teacher asks questions which I haven't prepared in advance | -0.15 | 0.73 |
| 30 | I feel overwhelmed by the number of rules you have to learn to speak a foreign language | -0.17 | 0.67 |
| 23 | I always feel that the other students speak the foreign language better than I do | -0.26 | 0.73 |
| 15 | I get upset when I don't understand what the teacher is correcting | -0.30 | 0.62 |
| 11 | I don't understand why some people get so upset over foreign language classes | -0.36 | 0.61 |
| 14 | I would not be nervous speaking the foreign language with native speakers | -0.46 | 0.62 |
| 8 | I am usually at ease during tests in my language class | -0.52 | 0.62 |
| 32 | I would probably feel comfortable around native speakers of the foreign language | -0.73 | 0.61 |
| 10 | I worry about the consequences of failing my foreign language class | -0.76 | 0.57 |
The item measures range from -0.76 to 0.68 logits, covering a rather narrow range of just 1.44 logits. The point measure correlations are all high (0.57 to 0.76). The items are very homogeneous and do not cover a wide range of the construct of interest.
A further examination of the semantics of the items revealed that quite a few items are semantically very similar, and this explains their narrow coverage. The most striking example is the following six items given in measure order from highest to lowest:
Item 20: I can feel my heart pounding when I'm going to be called on in language class.
Item 27: I get nervous and confused when I am speaking in my language class.
Item 9: I start to panic when I have to speak without preparation in language class
Item 24: I feel very self-conscious about speaking the foreign language in front of other students
Item 1: I never feel quite sure of myself when I am speaking in my foreign language class
Item 18: I feel confident when I speak in foreign language class
These six items have similar measures from -0.15 to 0.26 and lie within a range of just 0.41 logits. Also their point measure correlations are similar (0.63 to 0.76) with four of them being between 0.70 and 0.76. The above items cover the concept of uneasiness while speaking in the foreign language classroom. A final investigation on these items was the calculation of their inter-item correlations. Table 7 shows the results of this analysis.
Table 7
Inter-Item Correlations for Six Items
| Items | 1 | 9 | 18 | 20 | 24 | 27 |
|---|---|---|---|---|---|---|
| 1 | 1 | 0.521 | 0.492 | 0.519 | 0.482 | 0.545 |
| 9 | 1 | 0.577 | 0.613 | 0.498 | 0.626 | |
| 18 | 1 | 0.556 | 0.667 | 0.641 | ||
| 20 | 1 | 0.458 | 0.689 | |||
| 24 | 1 | 0.566 | ||||
| 27 | 1 |
All correlations lie between 0.458 and 0.689 and are highly significant (p < 0.01).
Another example of semantically similar items concerns items 14 (I would not be nervous speaking the foreign language with native speakers) and 32 (I would probably feel comfortable around native speakers of the foreign language). Items 14 and 32 had measures of -0.46 and -0.73 and point measure correlations 0.62 and 0.61. Finally the correlation between them was 0.533 (p < 0.01). Both items refer to the comfort or nervousness of students in speaking to native English speakers and not in the classroom setting.
The researchers believe that the high homogeneity of the items expressed by the narrow coverage of the construct, together with the inclusion of semantically equivalent items led to the misleadingly high reliability (alpha 0.958) in the preliminary analyses and by the person reliability (0.93).
Category Functioning
Table 8 shows the results of the investigation as to whether the scale used was optimal.
Table 8
Results of the Likert Scale Investigation
| Category | Label | Observed count | Observed average | Infit | Outfit | Thresholds |
|---|---|---|---|---|---|---|
| 1 | Strongly disagree | 2602 | -2.32 | 0.97 | 0.99 | None |
| 2 | Disagree | 2075 | -1.01 | 0.94 | 0.78 | -1.39 |
| 3 | Neither disagree nor agree | 1890 | -0.35 | 0.86 | 0.93 | -0.63 |
| 4 | Agree | 990 | 0.15 | 1.07 | 0.53 | 0.53 |
| 5 | Strongly agree | 350 | 0.57 | 1.33 | 1.50 | 1.50 |
Almost all criteria for optimal rating scale suggested by Linacre (2002) are satisfied. There are high observed frequencies in each category, the average measure increases monotonically along the categories, infit and outfit for all categories are well below 2.0 and close to 1.0, and the thresholds also increase monotonically indicating that each category is the most probable for a specific range on the construct continuum. However, the distances between consecutive thresholds are not all large enough to describe distinct ranges on the variable. Figure 5 shows the category probabilities.
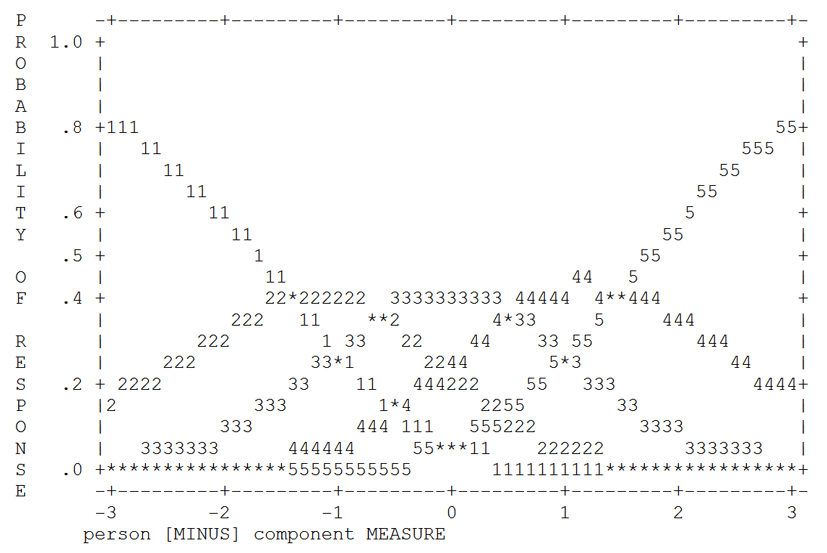
Figure 5
Category probabilities.
Each category peaks for some range along the continuum, however category 2 (disagree) is the most probable in a range of just 0.76 logits (from -1.39 to -0.63), category 3 (neither agree nor disagree) in a range of 1.16 logits (from -0.63 to 0.53) and category 4 (agree) in a range of 0.97 logits (from 0.53 to 1.50). The distance between the first and second thresholds is only 0.76 and is below 1.0 (Linacre, 2002) and between the third and fourth thresholds is 0.97, just below 1.0.
Since all other criteria for optimal category functioning are met, and all categories peak at some range on the variable continuum the fact that one category peaks at a range of 0.76 (below 1.0 as suggested by Linacre) is not a serious drawback thus the 5-point Likert scale can cautiously be considered optimal.
Discussion
The objective of this study was to evaluate the psychometric properties of the FLCAS. The Greek version was administered to a random sample of 304 students from three senior high schools in Limassol, Cyprus. Rasch analyses suggested that five items do not fit the model (infit and outfit values well above the critical value of 1.4). They were removed and the remaining 28 items constituted the scale used for the final analyses.
Research Question 1: Is the FLCAS a Unidimensional Scale?
For the investigation of the dimensionality of the 28-item FLCAS the following evidence was collected:
-
All item point measure correlations were high ranging from 0.57 to 0.76.
-
All but three items fit the Rasch model very well. The three items were slightly misfitting. However, it was shown that the inclusion of those items does not affect the validity of the person measures.
-
PCA of the standardised residuals showed that the major dimension measured by the scale explained more than 51% of the total variance in the data. More importantly however, the first factor extracted had an eigenvalue of 2.5, that is, the strength of two to three items. Further investigation on this was undertaken by contrasting the content of the three items with the highest positive loadings on this factor against the three items with the highest negative loadings. The two groups of items were not different in content. The second group simply contained reversed items. Furthermore, the dimension measured by the scale had approximately 12 times the strength of the first factor extracted and this factor explained only 4.4% of the total variance in the data.
All the evidence collected supports convincingly the assumption that the scale is unidimensional.
Having established the unidimensionality of the FLCAS, three more analyses were undertaken to clear up the discrepancy regarding whether test anxiety can be considered a component of FLCA (Horwitz et al. 1986; Tóth, 2008) or not (Aida, 1994; Cheng et al., 1999; Matsuda & Gobel, 2004). First the FLCAS was divided into two subscales, the FLTA (four items) and the remainder of the FLCAS (24 items). The correlation between the total scores on the two sub-scales was 0.831, which is highly significant. Second, person estimates were found using Rasch calibrations on two separate sets of data; the responses of the students to the full 28-item FLCAS and the 24-item FLCAS (excluding the four test anxiety items). The cross plot between the two sets of person measures revealed a very linear pattern and the correlation coefficient between them was 0.989. Finally, all the t-statistics for differences between the two different person estimates were found to lie well within the 95% confidence interval of -2 to 2, indicating no significant differences. These analyses show that test anxiety can be considered a component of FLCA.
Research Question 2: Does the FLCAS Provide Reliable Measures?
The preliminary reliability investigation revealed a very high internal consistency for the scale (alpha = 0.958). This high alpha was comparable with four primary studies on the FLCAS; Horwitz et al. (1986) found 0.93, Aida (1994) 0.94, Bekleyen (2004) 0.90 and Cao (2011) 0.95.
Such high alphas for psychometric scales may not be desirable (Boyle, 1985, 1991; Kline, 1979) as they could be an indication of parallel items or a narrow coverage of the construct being measured. These consequences of high internal consistency lower the validity of the scale.
Rasch analyses revealed similarly high reliability indices (person reliability 0.93, separation 3.64). The person-item map (Figure 3) depicts the problem. All items were positioned from -0.76 to 0.68 and this represents a narrow range, of just 1.44 logits, on the FLCA continuum. Also, the items are well targeted for persons with a measure above the mean (-1.06) and with a breadth of about one standard deviation of the person measures. Bora and Jongmin (2011) reported more precise and reliable person estimates for those in the low to medium anxiety levels. This study however shows the opposite, that items are well targeted (and thus giving more accurate estimates) for the medium to high anxiety students.
A close investigation revealed the existence of parallel items. The most striking example is the case of six semantically akin items with similar statistics (item estimates from -0.15 to 0.26 logits and point measure correlations from 0.63 to 0.76). All six items cover the concept of uneasiness while speaking in the FL classroom. The correlations between them were also all highly significant (p < 0.01) ranging from 0.482 to 0.689. This use of repeated items has two undesirable effects. First the breadth of measurement of the given construct is narrow because of high homogeneity of the items, thus lowering the degree of validity of the scale. Second, the scale may be contaminated by a bloated specific, where repeated coverage of semantically the same item leads to apparent high reliability and an unwanted common factor affecting the factor structure of the scale. Boyle (1991) argues that moderate to low homogeneity should be preferred in order to ensure a broad coverage of the construct being measured.
Research Question 3: Is the 5-point Likert Scale Psychometrically Optimal?
The 5-point Likert scale satisfied all but one criterion for being optimal. The distances between adjacent thresholds were not all greater than 1.0 logits as suggested by Linacre (2002). Two out of the three ranges were 0.97 (which is close enough to 1.0 to be considered just satisfactory) and 0.76 logits, marginally unsatisfactory. Perhaps by removing the neutral category and using a 4-point Likert scale (strongly disagree, disagree, agree, strongly agree) the problem will be solved.
Possible Limitations of the Study
While the sample of 304 high school students can be considered sufficiently large for reliable results, generalization to the whole population of Cypriot students is risky since the sample can only represent the population from which it was drawn, namely the students of Limassol.
Sechrest, Fay, and Hafeez Zaidi (1972) emphasised the importance of “equivalence in terms of experiences and concepts” (p. 41) when translating questionnaires. While every effort was made to produce an accurate translation of the instrument, slight semantic differences between the English and Greek versions of the FLCAS cannot be ruled out.
Unlike the majority of studies on the FLCAS the sample in this study consisted of high school students of 16 – 18 years of age who had been studying the foreign language (English) for most of their school lives. Most studies have investigated (near) beginners. This difference could account for the poor item targeting found in this study, but not for the narrow coverage of the construct since with the use of the Rasch models the item estimates are independent of the sample used.
Concluding Remarks and Suggestions
This study fills two important gaps in research. It is the first to validate the full 33-item FLCAS using the Rasch measurement and the first validation study, to the authors’ knowledge, to be conducted on a sample of high school students rather than university students.
The use of the Rasch approach clarified two discrepancies in the literature. First the factor structure of the FLCAS and second whether FLTA can be considered a component of FLCA. Results, after removing five misfitting items, strongly indicated that the scale is unidimensional and FLTA is a component of FLCA, therefore items related to FLTA need not be removed. Perhaps the two items (14 and 32) referring to the comfort or nervousness of students in speaking to native English speakers could be removed from the scale since they are not pertinent to the classroom setting.
The reliability of the scale was found to be high, in accordance with most primary studies on the FLCAS. It is perhaps questionably high, which is undesirable in psychometric scales since it lowers their validity. The investigation revealed two reasons for such a high reliability. First the items covered a rather narrow range on the variable continuum. Second, the scale includes many parallel items.
Further research into the refinement of the scale is strongly suggested, taking into consideration the following. First a careful semantic analysis of the remaining 28 items should be conducted in order to remove parallel or repetitive items. Second new easier (to endorse) items should be added in an attempt to achieve a wider coverage of the construct and to improve item targeting. This would raise the degree of validity of the scale and give more reliable person measures for the whole student population. The refined scale should be analysed to verify that its psychometric properties are maintained, or better yet, improved.
A final suggestion concerns the marginally optimal 5-point Likert scale. The statistics of this study direct towards a possible collapsing of two of the central three categories, however the semantics are inhibitory. “Neither agree nor disagree” cannot be collapsed with either “Disagree” or with “Agree”. It is suggested, with caution, that a 4-point scale could be used instead by removing the neutral category. This way the distances between adjacent thresholds will most probably increase over the minimum desirable length of 1.0 logit thus covering distinct ranges on the construct continuum.
 This is an open access article distributed under the terms of the Creative Commons
Attribution License (
This is an open access article distributed under the terms of the Creative Commons
Attribution License (