Reasoning following the tenets of normative models such as logic, probability theory, and Bayes´ theorem has proven to be difficult for humans (Gigerenzer, 2000). When reasoning involves sentences with negation the performance is even lower (Wason & Johnson-Laird, 1972). The present study investigates why this is the case. Khemlani, Orenes, and Johnson-Laird (2012a, 2012b) presented an extension of the Mental Models Theory (MMT) of human thought (Byrne & Johnson-Laird, 2009; Johnson-Laird, 1983, 2008) to account for the specific case of negation in sentences. The aim of this study was to test two hypotheses derived from such an account, and more generally, to shed light on the difficulties that humans face when reasoning with sentences containing negation. The first hypothesis is concerned with correct responses while the second deals with a possible generalized pattern of responses.
The article continues as follows. First, we present the core concepts of the MMT of human thought. Then, we define sentential reasoning and describe how the MMT explains this kind of mental processing. Then, we introduce comments on the mathematical logic of the negation of conjunctions and disjunctions. Then, we derive two hypotheses from a recent extension of the MMT that is specifically concerned with the negations of interest. Before presenting and discussing the experiment, we comment on the paradigm employed to test these hypotheses and introduce predictions derived from an alternative theory.
Mental Models Theory
The MMT successfully explains a broad range of reasoning phenomena (Johnson-Laird, 2008, 2010a). Deductive, inductive, and probabilistic reasoning are the main research fields covered by this analytic theory that emerged against the traditional theories of logical form (Johnson-Laird, 2010b). Such tradition includes the Mental Logic theories (Braine & O’Brien, 1998), the Psychology of Proof (Rips, 1994, 2011), and a number of accounts influenced by Piagetian formalism (Johnson-Laird, 2008, 2010b). The MMT argues that the objects studied by logic are radically different than the representations and inferences of human reasoning. Johnson-Laird (1983) postulated that reasoning phenomena are semantically-driven instead of rules-driven. According to the MMT reasoning depends on envisaging possibilities that are consistent with some given information (Johnson-Laird, 2010b). Such information comes from external sources through perception but also from internal sources like personal knowledge. In this context, mental models can be broadly defined as iconic representations of the world (Johnson-Laird, 2008). Mental models are dynamic constructions that initially represent only what is true and may or may not flesh out fully explicit models that also represent what is false (García-Madruga, Gutiérrez, Carriedo, Moreno, & Johnson-Laird, 2002). The MMT postulates that working memory has a critical importance for reasoning (Johnson-Laird, 1983). The simultaneous representation of a set of mental models would require the activation of working memory. The MMT argues that reasoning errors are the product of working memory overload. When the amount of representation increases, the working memory load is heavier. The probability of committing reasoning errors grows as the working memory load grows, according to the MMT (Johnson-Laird, 2008; Johnson-Laird & Byrne, 1991). Additionally, the MMT postulates that the human mind systematically tends to avoid working memory load (Johnson-Laird, 1983, 2008, 2010a). In a broad sense, the MMT suggests that lower mental efforts are preferable to higher mental efforts. This holds insofar as specific reasoning tasks are compatible with such economic behavior (Johnson-Laird, 2010b).
Sentential Reasoning
The general aim of the MMT is to account for the representation and inferential processing of human thinking. In particular, sentential reasoning is one of the central topics studied by the MMT. Sentential reasoning can be defined as the cognitive processing of propositions (Johnson-Laird, 2008). A proposition or sentence can be defined in this context as an expression that can be either true or false, but not both (Suppes & Hill, 1992). If a truth value cannot be attributed to a given expression, then such expression is not a sentence even if it makes sense in a particular language (Garnier & Taylor, 1996). A question, for example, is not a sentence. Several links between sentences can be established through connectives. These connectives are abstract logical functions that are represented in human language through words like and, and or to express conjunction and disjunction, respectively (Springston & Clark, 1973). The word not has also logical and psychological importance because it expresses negation. Another important connective is the conditional that takes the form of if…, then… (Byrne & Johnson-Laird, 2009; García-Madruga et al., 2002). Mathematical logic further postulates that an atomic sentence is one that lacks connectives and the operator of negation, whereas a molecular sentence is one that includes connectives linking two or more atomic sentences and admits operators like negation (Suppes & Hill, 1992). For example, the expression “London is a city” is an atomic sentence, which can be represented by a small letter (e.g., p) (Garnier & Taylor, 1996). “Africa is a continent” is another atomic sentence, which can be represented by another small letter (e.g., q). Some operations can be performed between p and q to construct molecular sentences. For example, “London is a city and Africa is a continent” is a molecular or compound sentence because two atomic sentences are brought together through the conjunction expressed by the word and. The conjunctive expression p and q represents an abstraction of the latter molecular sentence.
Working Memory Load in Sentential Reasoning
The MMT provides a method to account for the working memory load in sentential reasoning (Johnson-Laird, 1983, 2008). This method postulates a correspondence between a given connective and the number of mental models needed to represent it psychologically (García-Madruga et al., 2002). Table 1 presents a summary of this assignation for the main connectives in sentential reasoning for any p and q atomic sentences.
Table 1
Mental Models for the Main Connectives.
| Connective | Sentential Form | Mental Models | Working Memory Load | |
|---|---|---|---|---|
| Conjunction | p and q | p | q | 1 |
| Exclusive disjunction | p or else q | p | 2 | |
| q | ||||
| Conditional | if p, then q | p | q | 2+ |
| ... | ||||
| Inclusive disjunction | p or q, or both | p | 3 | |
| q | ||||
| p | q | |||
Note. The Working Memory Load depends on the number of Mental Models needed to represent a given connective (Johnson-Laird, 1983, 2008). Each Mental Model is represented by one row (Byrne & Johnson-Laird, 2009).
Given a sentence, the MMT abstracts its sentential form. For example, given the molecular sentence “London is a city and Africa is a continent”, the sentential form would be p and q. This form can be represented through a single row that includes the letters p and q according to the MMT (Byrne & Johnson-Laird, 2009). The working memory load for this case corresponds to one mental model because only one possibility is yielded by the conjunctive connective: a world in which both p and q are true. The working memory load increases for the exclusive disjunction, as shown in Table 1. This connective needs two mental models to represent the situation in which p is true or else q is true. For example, the sentence “London is a city or else Africa is a continent” requires the mental representation of two possibilities. In one possible world it is the true that London is a city. In the other possible world it is true that Africa is a continent. Each possibility excludes the alternative possibility in the exclusive disjunction case (Suppes & Hill, 1992).
According to the MMT the psychological representation of conditionals is a special case (Byrne & Johnson-Laird, 2009; Schroyens, Schaeken, Fias, & d’Ydewalle, 2000). Only one case is explicitly considered, that is, the particular case of being p and q both true for sentences of the form if p, then q. Mathematical logic states that a conditional is also true when the antecedent p is false (Garnier & Taylor, 1996), no matter the truth value of the consequent q. Nevertheless, the MMT conjectures that only a tacit representation of these false antecedent cases is psychologically represented (Evans & Over, 2004; García-Madruga et al., 2002). For example, the sentence “If London is a city, then Africa is a continent” promotes the mental representation of only one explicit possibility in which London is a city and Africa is a continent. However, the conditional connective is compatible with other possibilities. If London were not a city, then the conditional would still be true. That is, a reasonable representation of a conditional admits a possibility in which p is false and q is true. The same situation occurs when p is false and q is false: the conditional is still true (Schroyens et al., 2000). Hence, the sentential form if p, then q yields three possibilities when the models are fully fleshed out. Nevertheless, the MMT postulates that only one possibility is explicitly represented by humans (García-Madruga et al., 2002). A second possibility is implicitly represented, that is, individuals figure out that some other cases would be acceptable, but only their eventual occurrence is considered. In sum, the conditional connective loads the working memory with two situations, one is explicit and the other is implicit. The implicit situation (see plus sign in Row 3 of Table 1) represents a set of possibilities. Finally, the inclusive disjunction connective yields a working memory load of three mental models. One possibility is that p is true, another possibility is that q is true. The third possibility is that both p and q are true.
DeMorgan´s Laws
Two logical laws attributed to Augustus DeMorgan (1847) state equivalences of interest for the negation of conjunctions and disjunctions based on mathematical proof (Suppes & Hill, 1992). Two sentences are equivalent when they are interchangeable because both have the same abstract truth values distribution (Garnier & Taylor, 1996). DeMorgan´s law 1 state that not (p and q) is equivalent to (not p) or (not q). DeMorgan´s law 2 state that not (p or q) is equivalent to (not p) and (not q). An example for law 1 is the equivalence between the sentence “It is not the case that: London is a city and Africa is a continent” and the sentence “London is not a city or Africa is not a continent”. An example for law 2 is the equivalence between “It is not the case that: London is a city or Africa is a continent” and “London is not a city and Africa is not a continent”. According to DeMorgan´s laws the negation of a conjunction is a disjunction. The negation of a disjunction is, conversely, a conjunction. It is important to note that DeMorgan´s laws apply only to the inclusive case of disjunction, that is, the disjunction that admits the case of two true atomic sentences (Garnier & Taylor, 1996).
The Mental Models Theory of Negation
An extension of the MMT concerned with negation has been proposed by Khemlani et al. (2012a). This theory defines negation as the operation that returns the complement of a given single argument. Negation operates, for example, on a given sentence, atomic or molecular. This definition replicates in the context of the MMT the meaning of the mathematical function of complementation in set theory (Suppes & Hill, 1992). One of the main predictions formulated by this extension of the MMT states that the negation of conjunctions is psychologically harder to represent and to understand than the negation of disjunctions (Khemlani et al., 2012a, Prediction 5). This would happen because the former loads heavier on the working memory than the latter. The inclusive disjunction requires three mental models while the conjunction requires only one mental model, as is shown in Table 1.
The Selection Paradigm Facilitates the Working Memory Load Evaluation
Two experimental paradigms have been historically applied for the study of sentential reasoning: the selection paradigm and the construction paradigm (Wason & Johnson-Laird, 1972). The main purpose of the selection paradigm is to study inferences, whereas the construction paradigm aims to study representations (Sevenants, Dieussaert, & Schaeken, 2011). In this context selection means that a set of response options is given, and experimental participants have to choose one option. Construction means, by contrast, that no options are given, and participants have to produce their own responses. One important aspect of the selection paradigm is the possibility to control the form of all the response options because such set can be closed by design. For example, the working memory load can be experimentally controlled and evaluated for each response option. On the other hand, in the construction paradigm the set of possible responses remains open.
Alternative Theories
Theories of deduction based on formal rules like Mental Logic (Braine & O’Brien, 1998) or the Psychology of Proof (PSYCOP; Rips, 1994, 2011) predict different reasoning patterns than those of the MMT of negation (Khemlani et al., 2012a, 2012b). The core assumption of PSYCOP is that sentences entered into human working memory are scanned by a set of formal rules akin to those studied by logic. These rules can work forwards or backwards. The former applies when premises are given and a conclusion entailment is sought. The latter corresponds to tasks that also include the conclusion and require a coherence analysis between such conclusion and a given set of premises. Hence, forward rules are concerned with production tasks while backward rules apply for evaluation tasks. When a selection paradigm is employed, the backwards case would be the appropriate theory to derive predictions. Rules in PSYCOP can be understood as inference routines (i.e. algorithms). The routine required for backward DeMorgan´s laws predict no difference in working memory load between law 1 and law 2. Both rules need 4 steps including the construction of logical structures like domains, goals, and formulas that host the specific processes of compound negation. The backward steps for law 1 are: “a) Set D to domain of current goal. b) If current goal is of the form (NOT P) OR (NOT Q), c) and NOT (P AND Q) is a subformula of a sentence that holds in D, d) then add NOT (P AND Q) to the list of subgoals” (Rips, 1994, p. 118). The backward steps for law 2 are: “a) Set D to domain of current goal. b) If current goal is of the form (NOT P) AND (NOT Q), c) and NOT (P OR Q) is a subformula of a sentence that holds in D, d) then add NOT (P OR Q) to the list of subgoals” (Rips, 1994, p. 118). Contrarily, when the task requires a conclusion entailment, the prediction of PSYCOP for DeMorgan´s laws is that three forward steps are needed for law 1 (Rips, 1994, p. 113) and five for law 2 (Rips, 1994, p. 114). This is the opposite than that of the MMT of negation.
Other relevant studies concerned with negation have been conducted in linguistics. Some authors argue that negation is pragmatically different than affirmation (Horn, 1989) while others argue against such asymmetry (Giora, 2006). More specifically, some experimental pragmatics studies contributed evidence concerned with scalar implicature (i.e. negation phenomena based on the modulation of different degrees of informativeness that can be observed in conversational contexts, Katsos & Cummins, 2010). For example, the expression “Some professors are famous” admits the interpretation that not all the professors are famous (Papafragou & Musolino, 2003). Nevertheless, the term some admits any case of a theoretical informativeness scale that includes all the professors in one side and only two professors in the opposite side. The accumulated evidence obtained in experimental pragmatics studies showed that the specific interpretation of such expressions is affected by developmental factors (Papafragou & Musolino, 2003), discourse goal, and the epistemic state of the subjects who take part in the conversation (Katsos & Cummins, 2010). In sum, a pragmatic approach to this communications suggests that scalar implicatures are context-dependent implicit negations. Further research is needed to elaborate on the relation between negations of compound sentences like the ones proposed in this study and scalar implicature. To advance in such direction the experimental materials should be accommodated to include quantifiers that were omitted in this study like all, some, not all, not some.
Hypotheses
The aim of the present contribution is to test two hypotheses derived from the MMT for the particular case of the negation of conjunctions and disjunctions in a selection task that apply DeMorgan´s laws. Hypothesis H1 states that the recognition of a logical equivalence for the negation of a conjunction (DeMorgan´s law 1) is harder to achieve than the recognition of a logical equivalence for the negation of a disjunction (DeMorgan´s law 2). Hypothesis H1 follows the novel prediction proposed by Khemlani et al. (2012a, 2012b) in the context of the MMT of negation. These authors argue that negating a conjunction is harder than negating a disjunction because the former requires more mental models and more working memory load than the latter. Hypothesis H1 is concerned with correct responses. Hypothesis H2 elaborates on the same conjecture but also considers incorrect responses. Hypothesis H2 states that overall responses to the task of interest follow a psychological pattern configured by the working memory load such that the most frequent responses are those linked to lower loads. This conjecture is derived from the MMT principle that considers the human mind as computationally economic, that is, prone to avoid unnecessary efforts during reasoning (Johnson-Laird, 2008).
Method
Participants
79 undergraduate students were randomly recruited at a public university located at the city of Paraná, Argentina. All the participants were social sciences students who had no formal education in mathematics or logic. The mean age was 25.05 years old (SD = 4.56). Female participants (n = 69) represented 87.3% of the sample.
Design
A within-subjects experimental design was applied to compare the participant’s performance in tasks that require the recognition of DeMorgan´s laws. All participants were given a reasoning task of eight items, of which four applied law 1 and the other four applied law 2. The independent variable was defined as the logical form of the materials (law 1, law 2). Law 1 condition defines operationally the equivalence for the negation of a conjunction, whereas law 2 condition corresponds to the equivalence for the negation of a disjunction. The dependent variable was defined as the number of correct responses. Incorrect responses were also considered for further analysis.
Materials and Procedure
Participants were given a paper and pencil task that required the recognition of a logical equivalence for the negation of a conjunction or the negation of a disjunction. Table 2 presents an example of the experimental task.
Table 2
Experimental Task Example
| Instructions: please find the sentence in small letters that is equivalent to the sentence in capital letters. Two sentences are equivalent when they have the same abstract meaning. Please note that the task does not require finding which small letters sentence is true, or false. The task requires selecting the sentence in small letters that expresses exactly the same idea as the sentence in capital letters. Only one of the four response options is correct. |
|---|
IT IS NOT TRUE THAT: LONDON IS A CITY AND AFRICA IS A CONTINENT
|
Note. The asterisk shows the correct response. This sentence in English intends to translate the inclusive disjunction presented in Spanish to the experimental subjects. The materials applied excluded the expression “or both” suggested by García-Madruga et al. (2002), but were clear for the experimental subjects about the inclusive condition.
The task was to read first the sentence written in capital letters (see Table 2), which was structured as the negation of a conjunction (4 items) or the negation of a disjunction (4 items). After reading that sentence, participants were asked to select one of the options written in small letters (see Table 2). They were also instructed that one and only one of the given options was the logical equivalent of the sentence in capital letters. Both the sequence of eight items and the sequence of four options within each item were randomized. The construction of atomic sentences was controlled by design to cover all the possible combinations of truth values. That is, the pairs of atomic sentences for law 1 were TT (true, true), TF (true, false), FF, FT, before randomization. The same strategy was applied for law 2. The aim of this materials design was to study the response patterns to this restricted universe of truth values and to complementary evaluate the possible occurrence of the belief bias, understood as the tendency to respond to logic tasks on the basis of world knowledge, rather than on the required formal criterion (Evans & Curtis-Holmes, 2005). The psychometrical reliability was acceptable (Fleiss, Levin, & Paik, 2004) for the 4 items constructed for law 1 (Cronbach´s α = 0.595) and for the 4 items corresponding to law 2 (Cronbach´s α = 0.814).
Items structured after law 1 included response options for the exclusive disjunction, the conditional, and the conjunction, besides the correct response (inclusive disjunction). For law 2 the response options were the exclusive disjunction, the conditional, the inclusive disjunction, and the correct response (conjunction).
The sessions lasted about 10 minutes. The sessions recruited groups of 20 to 30 students in regular courses at the beginning of a lesson, and were conducted with the corresponding institutional authorizations. Before starting the experiment, the invited students received a brief explanation about the research and voluntarily signed a consent form.
Results
Measures
Recognition is operationally defined as the number of correct selections for each law per participant and fluctuates between 0 and 4 because four items for each law were included in the experimental task. This variable was applied to test hypothesis H1. Response Indexes are measures of responses that were applied to test hypothesis H2. Four indexes were constructed: the Surface-Index, the Scope-Index, the Transformation-Index, and the Correct-Index. The Surface-Index is the sum of responses that negate the atomic sentences and preserves the connectives structure, within each participant. That is, the Surface-Index is the sum of the responses that have the abstract form of (not p) and (not q) to law 1 or (not p) or (not q) to law 2. This response is classified as superficial because it operates only on the atomic sentences, but does not modify the connectives structure. The Scope-Index is the sum of selections that have the abstract form of (not p) or (not q), within each participant. The same rule is applied for both DeMorgan´s laws to construct the Scope-Index. The name of the index was chosen because the difference between the inclusive disjunction and the exclusive disjunction is on their respective scope (Suppes & Hill, 1992), but only the former is compatible with DeMorgan´s laws. The Transformation-Index is the sum of selections of the conditional form with both the antecedent denied, and the consequent denied (i.e., if (not p), then (not q)), within each participant. This response option was included in the experimental task because a conditional can be transformed into a disjunction according to mathematical logic (Garnier & Taylor, 1996). A Correct-Index was also calculated for the sum of correct choices in each participant. This vector received 1 point if the response form to law 1 was (not p) or (not q), or the response to law 2 was (not p) and (not q). In sum, four indexes were calculated for each participant to test hypothesis H2, three for incorrect responses and one for the correct response. These indexes are vectors with values that range from 0 to 8 because the experimental task includes 8 items and each item includes response options for the 4 indexes of interest.
The effect size estimator chosen was Cliff´s δ, which yields real numbers between minus 1 and plus 1, with zero being the absence of an effect (Macbeth, Razumiejczyk, & Ledesma, 2011). The plus 1 and minus 1 polarities are indicators of the maximum effect size. The sign depends only on which vector was entered first to the algorithm. Hence, the polarity can be neglected without information lost. Consequently, the absolute value for the Cliff´s δ is given. A small Cliff´s δ is around 0.147, a medium δ is around 0.33 and a large δ is around 0.474 (Romano, Kromrey, Coraggio, Skowronek, & Devine, 2006).
Data Analysis and Discussion
No statistical differences were found between male and female participants after Mann-Whitney U test for DeMorgan´s law 1 Correct-Index (z = -0.147, p = .883, |Cliff´s δ| = .01), DeMorgan´s law 2 Correct-Index (z = -0.352, p = .725, |Cliff´s δ| = .06), the Surface-Index (z = -0.429, p = .668, |Cliff´s δ| = .08), the Scope-Index (z = -0.753, p = .452, |Cliff´s δ| = .13), and the Transformation-Index (z = -0.862, p = .389, |Cliff´s δ| = .11). The resulting lack of difference between male and female participants in DeMorgan´s reasoning tasks is consistent with previous studies on verbal reasoning (Colom, Contreras, Arend, García Leal, & Santacreu, 2004).
The observed response vectors were incompatible with the normality assumption after Kolmogorov-Smirnov´s test. Consequently, non-parametric statistics were applied. Tables 3 and 4 introduce descriptive statistics for overall responses to law 1 and law 2, respectively. Figures 1 and 2 introduce visual statistics for the same results.
Table 3
Response Pattern for DeMorgan´s Law 1
| Response | Mean | Standard Deviation | Working Memory Load |
|---|---|---|---|
| Surface-Index | 3.25 | 1.17 | 0 |
| Scope-Index | 0.42 | 0.91 | 2 |
| Transformation-Index | 0.22 | 0.65 | 2+ |
| Correct-Index | 0.11 | 0.32 | 3 |
Note. The Working Memory Load was operationally defined as the number of mental models linked to each Index. The Surface-Index aimed to capture superficial responses and was consequently associated to the absence of mental models. The Scope-Index option took the form of an exclusive disjunction with 2 mental models. The Transformation-Index option was formulated as a conditional with 2 mental models (Johnson-Laird, 2008). The plus symbol means that one of these two models was tacit, which required additional processing. The Correct-Index was constructed as an inclusive disjunction with 3 models. This mental models description follows García-Madruga et al. (2002) and was introduced in Table 1.
Table 4
Response Pattern for DeMorgan´s Law 2
| Response | Mean | Standard Deviation | Working Memory Load |
|---|---|---|---|
| Surface-Index | 1.78 | 1.61 | 0 |
| Correct-Index | 1.28 | 1.49 | 1 |
| Scope-Index | 0.73 | 1.21 | 2 |
| Transformation-Index | 0.20 | 0.51 | 2+ |
Note. The Working Memory Load assignations were explained in the Note of Table 3.
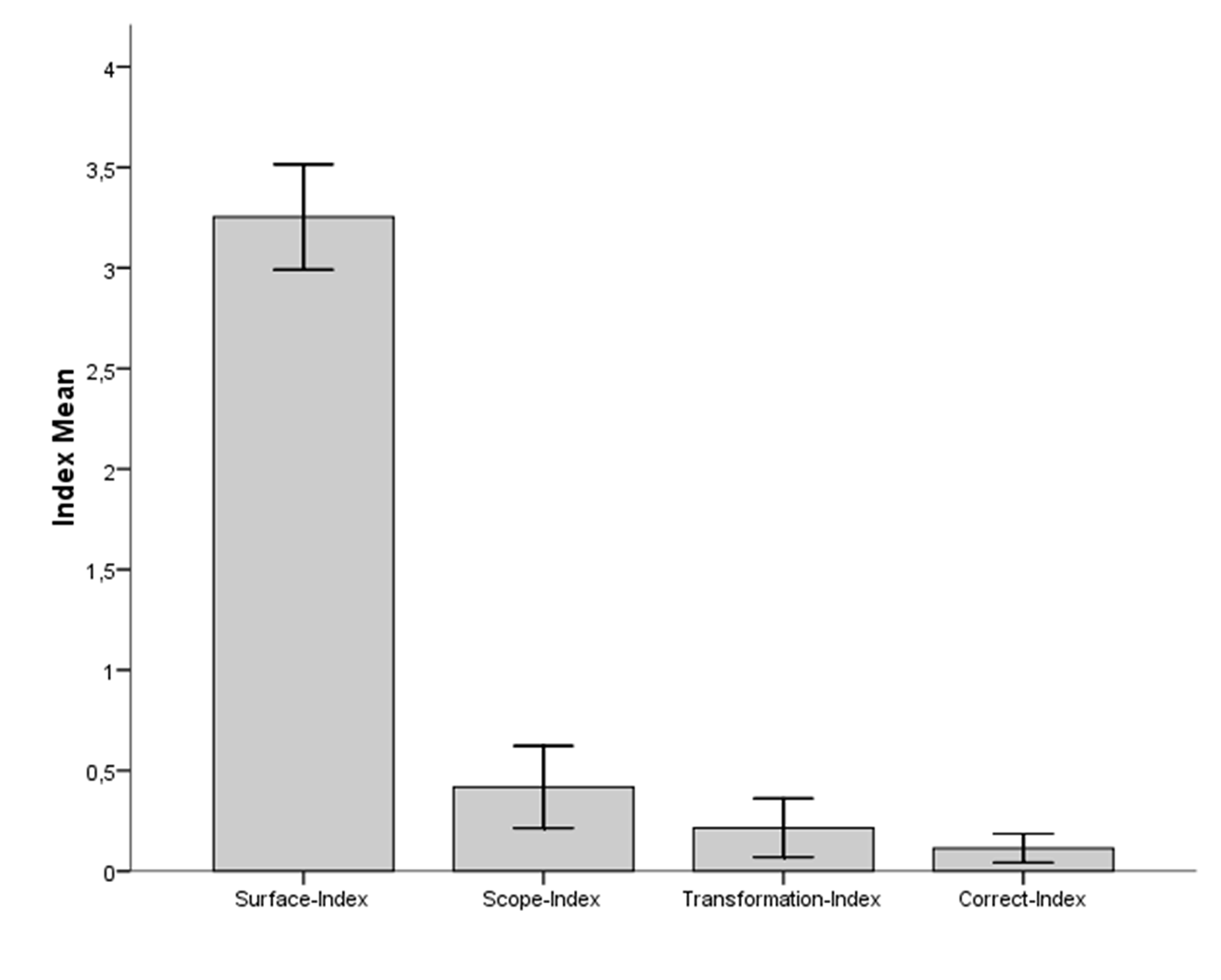
Figure 1
General response pattern for law 1. Error bars represent a 95% confidence interval for the mean.
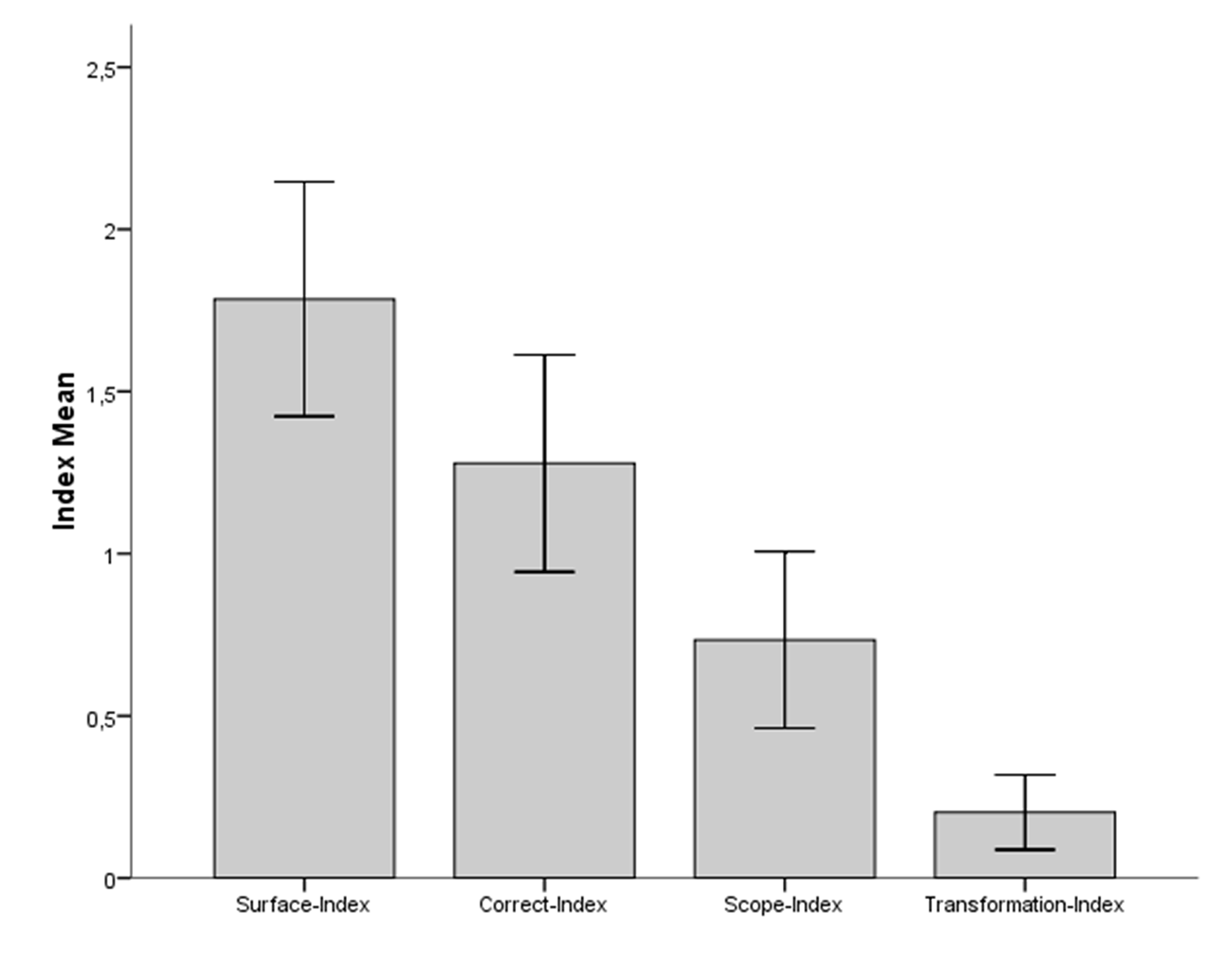
Figure 2
General response pattern for law 2. Error bars represent a 95% confidence interval for the mean.
DeMorgan´s law 1 (mean = 0.11; SD = 0.32) was harder to recognize than DeMorgan´s law 2 (mean = 1.28; SD = 1.49). This result is consistent with hypothesis H1 (Sign test, z = -5.276, p < .001, |Cliff´s δ| = .458, large effect size) and supports the theory of negation based on the MMT proposed by Khemlani et al. (2012a, 2012b). This may occur because law 1 refers to an inclusive disjunction and law 2 refers to a conjunction. Conjunctions have only one mental model while disjunctions have three mental models for the inclusive case employed in the present study as correct response for law 1 (García-Madruga et al., 2002). Processing three mental models is more difficult than processing only one mental model because the former loads heavier on working memory than the latter.
These experimental results are inconsistent with the prediction of PSYCOP both for backward and forward DeMorgan´s rules. The backward version predicts no difference between law 1 and law 2 while the forward version predicts more difficulty for law 2 than for law 1. The evidence contradicts both predictions.
The general response pattern was also modulated by the working memory load as predicted by hypothesis H2. A collective statistical test for the observed general response pattern presented in Tables 3 and 4 and Figures 1 and 2 was applied to evaluate H2. Results suggest that the most frequent responses were those associated with fewer mental models for law 1 (Friedman test, n = 79, df = 3, Χ2 = 149.22, p < .001) and for law 2 (Friedman test, n = 79, df = 3, Χ2 = 43.28, p < .001).
The most frequent response to both rules was the Surface-Index. This result can be interpreted as the product of a superficial processing analogous to the matching bias in the Wason Selection Task (Evans, 1998). The MMT of negation predicted this phenomenon for the negation of conjunctions and disjunctions. Khemlani et al. (2012a) proposed that negation has a small scope, that is, its operation is spontaneously restricted to the atomic components rather than connectives. This might be the most frequent response because it requires the lowest working memory load among the response alternatives (Macbeth, Razumiejczyk, Crivello, Fioramonti, & Pereyra Girardi, 2013).
In sum, the working memory load modulated the processing of sentential negation for conjunctions and disjunctions. When fewer mental models were required by a response option, more selections were made for that option. This result is compatible with previous experiments that accounted for conjunctive and disjunctive inferences applying MMT predictions (García-Madruga, Moreno, Carriedo, Gutiérrez, & Johnson-Laird, 2001).
General Discussion
Sentential negations are psychologically difficult. Wason and Johnson-Laird (1972) found that negative statements are harder to deal with than false statements and Giora (2006) claims that negation depends on high-level cognitive machinery. Such difficulty may stem not only from cognitive factors but also from structural conditions of negation per se. Further research is needed to elaborate on the relation between implicit quantified negation of scalar implicature and the negation of conjunctions and disjunctions considered in this study.
The MMT extension proposed by Khemlani et al. (2012a, 2012b) to account for the negation operator includes a novel prediction for the processing of DeMorgan´s laws in sentential reasoning. Such prediction states that the negation of a conjunction should be harder to process than the negation of a disjunction. This would happen because the negation of a conjunction is logically equivalent to an inclusive disjunction (DeMorgan´s law 1), which requires three mental models. The negation of an inclusive disjunction is logically equivalent to a conjunction (DeMorgan´s law 2), which requires only one mental model. Processing three mental models is harder than processing one mental model because the former requires more working memory load than the latter. The results of the present study are consistent with this MMT prediction.
This study has a number of limitations regarding the material. First, given that only concrete materials were used, further research is needed to test the same conjectures with abstract materials. This is because previous studies found differences in performance between concrete and abstract material in a variety of reasoning tasks (Wason & Johnson-Laird, 1972). Second, some sentences may have sounded awkwardi to the experimental participants and some sentences are counter-factual. The adjustment of these expressions to obtain more fluent or natural language sentences is recommended for further studies. The counter-factual condition of some sentences was controlled by design. The aim of this design was to test the possible contribution of the belief bias to the Correct-Index responses (Evans & Curtis-Holmes, 2005). That is, participants may respond differently to sentences that contradict their world knowledge when compared to sentences that are consistent with their world knowledge. Four given compound sentences were true and four were false. The true sentences were structured as “It is not true that:” “F or F”, “T and F”, “F and T”, “F and F”. The false sentences were structured as “It is not true that:” “T and T”, “F or T”, “T or T”, “T or F”. A True-Index was defined as the sum of correct responses to the true sentences, whereas a False-Index was the sum of correct responses to the false sentences. The comparison between these indexes for factual (True-Index mean = 0.41, SD = 0.543) and counter-factual (False-Index mean = 0.99, SD = 1.182) compound sentences yielded nonsignificant results (Sign test, z = -3.843, p < .001, |Cliff´s δ| = .221, small effect size). This result suggests that the belief bias did not affect the responses to the negations task. This expected effect was probably not found because the task in our experiment was to recognize equivalences, which are tautological biconditionals, while the belief bias has been observed in syllogisms. Furthermore, our task did no employ quantifiers while the experiments of Evans and Curtis-Holmes (2005) that increased the belief bias under time constraints were focused on quantifiers. A recent contribution found that belief bias is stronger when reasoning is more difficult (Brisson, de Chantal, Forgues, & Markovits, in press). Hence, for future studies focused on the relation between negation and belief bias the experimental control of task difficulty is recommended.
Results support the conjecture that predicted an inverse relation between the number of mental models required to represent different connectives and the number of correct choices. The most selected options were those associated with fewer mental models. Such tendency was observed for both DeMorgan´s laws. These findings are compatible with the MMT postulate concerned with the spontaneous dynamics of mental computations. According to this postulate, the human mind tends to avoid cognitive load insofar as the required task is compatible with such behavior. This view is compatible with an ecological approach to the study of human reasoning focused on environmental adjustment through low demanding mental computations (Gigerenzer, Todd, & ABC Research Group, 1999).
Another limitation of this study is the lack of chronometrical evidence. A response time analysis is needed to provide a further evaluation of the Surface-Index responses. If such responses are superficial and the other options are simultaneously neglected, then the response time for the Surface-Index responses should be shorter than the response time of other options. This evidence would give stronger empirical support to the proposed theory-driven construction of the Surface-Index linked to zero mental models. Further research is needed to account for the conditions under which this kind of processing is activated. About this issue Gilhooly (2005) proposed a general conjecture that predicts simpler processing strategies as reasoning tasks become more complex (Stupple, Ball, & Ellis, 2013).
In sum, the present contribution provides complementary evidence to the theory of negation proposed by Khemlani et al. (2012a, 2012b) in the context of the MMT for the particular cases of conjunctions and disjunctions. Additionally, this study provides novel evidence for the conjecture that predicts a general response pattern modulated by the working memory load for the negations of interest. Both results are consistent with the MMT postulate of computational economy applied to the particular case of DeMorgan´s laws.
 This is an open access article distributed under the terms of the Creative Commons
Attribution License (
This is an open access article distributed under the terms of the Creative Commons
Attribution License (